Operaciones con Matrices.

Introducción:

¿Qué son?

Una matriz es un arreglo en forma rectangular de números ubicados en filas y columnas. Donde cada celda en una matriz se llama componente y puede ser cualquier número real, su tamaño se delimita por el número de filas y columnas

N x M ::

Donde N: Número de filas
M: Número de columnas

* El orden es importante porque le primer factor siempre representa al número de filas

Cuando el número de filas y el número de columnas coinciden su matriz es cuadrada (2x2); (3x3); (49x49), hay otros casos en donde no coinciden donde estas pueden ser de carácter; (5x4) ;(9x8); etc...

Suma de matrices:

La suma de matrices está definida solamente cuando ambas están compuestas por igual número de filas y número de columnas, del mismo orden o tamaño

[A] 2x3 + [B] 2x3 = [C] 2x3

Ejemplo:

· Propiedades de la suma de matrices:

Conmutativa: A+B= 0; Donde el orden de las matrices no afecta el resultado
Asociativa: A+(B+C)= (A+B)+C; Donde la forma de agrupar cada dos términos o más de la matriz no produce ningún cambio.
Distributiva: α ( A+B) = αA + αB; El escalar α multiplicado por una, o la suma de dos matrices se distribuye uniformemente.
Elemento neutro: A + 0 = A; Donde 0 es la matriz nula del mismo tamaño que la matriz A.
Elemento opuesto: A + (−A) = 0; La matriz opuesta es aquella en que todos los elementos están cambiados de signo.

Tutorial suma de matrices:

https://www.youtube.com/watch?v=Jy8MESucw6o

Resta de matrices:

La resta de matrices de igual manera está definida solamente cuando ambas están compuestas por igual número de filas y número de columnas, del mismo orden o tamaño.

[A] 1x6 - [B] 1x6 = [C] 1x6

· Propiedades de la resta de matrices:

Conmutativa: A - B= 0; Donde el orden de las matrices no afecta el resultado
Asociativa: A-(B-C)= (A-B)-C; Donde la forma de agrupar cada dos términos o más de la matriz no produce ningún cambio.
Distributiva: α ( A-B) = αA - αB; El escalar α multiplicado por una, o la suma de dos matrices se distribuye uniformemente.
Elemento neutro: A - 0 = A; Donde 0 es la matriz nula del mismo tamaño que la matriz A.
Elemento opuesto: A - (−A) = 0; La matriz opuesta es aquella en que todos los elementos están cambiados de signo.

Tutorial resta de matrices:

https://www.youtube.com/watch?v=oKoLR7qhf9s

Multiplicación de un escalar por una matriz:

Sea A=(aij) mxn

Escalar: α € Ɍ

Ax α = (αaij) mxn

Una matriz y un escalar so multiplicables en cualquier momento, donde cada término de la matriz se multiplica por el escalar, en forma de propiedad asociativa

Tutorial multiplicación de matriz por escalar(número real)

https://www.youtube.com/watch?v=Dcm9uUybmNU

Propiedades del producto escalar

Modulativa: Ax1=A
Ax0= 0 Matriz nula
Conmutativa: El orden de los factores de la multiplicación no latera el producto Ax α = αxA
Distributiva: α(A+B) = αA+ αB

Multiplicación de matrices:

Dadas las matrices:

Esta forma de disponer los vectores es la adecuada para definir la multiplicación entre matrices.

Dos matrices pueden multiplicarse si y solo si, el número de columnas de a es igual al número de filas de la segunda matriz (b).

Am x n x Bn x p = Cm x p

Así los elementos cij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos.

Ejemplo:

Tutorial multiplicación de matrices:

https://www.youtube.com/watch?v=szwRmj2YEjg

· Propiedades del producto de matrices

Asociativa: A* (B * C) = (A * B) * C
Elemento neutro: A * 1 = A; Donde 1 es la matriz identidad del tamaño que la matriz A.
Distributiva del producto respecto de la suma: A * (B + C) = A * B + A * C
No es Conmutativa: A * B ≠ B * A; Dado que el orden de los factores si altera el producto

Resolución de sistema de ecuaciones:

De:

Monasterio, D. M. (2009). Monografias.com. Obtenido dehttp://www.monografias.com/trabajos72/resolucion-sistemas-metodo-gauss-jordan/resolucion-sistemas-metodo-gauss-jordan2.shtml#bibliograa

Método Gauss- Jordan

Un método por el cual pueden resolverse sistemas de ecuaciones lineales con n números de variables, encontrar matrices y matrices inversas, en este caso desarrollaremos la primera aplicación mencionada.

Para resolver sistemas de ecuaciones lineales aplicando este método, se debe en primer lugar anotar los coeficientes de las variables del sistema de ecuaciones lineales en su notación matricial:

Entonces, anotando como matriz (también llamada matriz aumentada):

Una vez hecho esto, a continuación se procede a convertir dicha matriz en una matriz identidad, es decir una matriz equivalente a la original, la cual es de la forma:

Esto se logra aplicando a las distintas filas y columnas de las matrices simples operaciones de suma, resta, multiplicación y división; teniendo en cuenta que una operación se aplicara a todos los elementos de la fila o de la columna, sea el caso.

Obsérvese que en dicha matriz identidad no aparecen los términos independientes, esto se debe a que cuando nuestra matriz original alcance la forma de la matriz identidad, dichos términos resultaran ser la solución del sistema y verificaran la igualdad para cada una de las variables, correspondiéndose de la siguiente forma:

· d1 = x

· d2 = y

· d3 = z

Ahora que están sentadas las bases, podemos explicar paso a paso la resolución de sistemas de ecuaciones lineales por medio de este método.

Para ilustrarnos mejor lo analizaremos con un ejemplo concreto:

· Sea el sistema de ecuaciones:

· Procedemos al primer paso para encontrar su solución, anotarlo en su forma matricial:

· Una vez hecho esto podemos empezar a operar con las distintas filas y columnas de la matriz para transformarla en su matriz identidad, teniendo siempre en cuenta la forma de la misma:

· Lo primero que debemos hacer es transformar el 2 de la 1ª fila de la matriz original en el 1 de la 1ª fila de la matriz identidad; para hacer esto debemos multiplicar toda la 1ª fila por el inverso de 2, es decir ½.

· Luego debemos obtener los dos ceros de la primera columna de la matriz identidad, para lograr esto, buscamos el opuesto de los números que se ubicaron por debajo del 1 de la primera columna, en este caso el opuesto de 3 que será -3 y el opuesto de 5 que será -5.

Una vez hecho esto, se procederá a multiplicar los opuestos de estos números por cada uno de los elemento de la 1ª fila y estos se sumaran a los números de su respectiva columna. Por ej.: en el caso de la 2º fila, se multiplicara a -3 (opuesto de 3) por cada uno de los elementos de la 1º fila y se sumara su resultado con el número que le corresponda en columna de la segunda fila. En el caso de la 3ª fila se multiplicara a -5 (opuesto de 5) por cada uno de los elementos de la 1º fila y se sumara su resultado con el número que le corresponda en columna de la tercera fila.

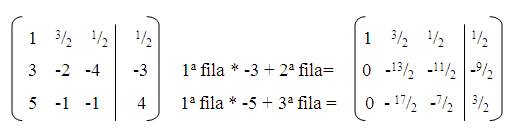
· Nuestro siguiente paso es obtener el 1 de la 2ª fila de la matriz identidad, y procedemos de igual forma que antes, es decir multiplicamos toda la fila por el inverso del número que deseamos transformar en 1, en este caso -13/2, cuyo inverso es -2/13

Además si observamos la tercera fila, nos damos cuenta que todos los elementos poseen el mismo denominador, entonces podemos eliminarlos multiplicando todos los elementos de la 3º fila por 2 (el denominador); si bien este no es un paso necesario para el desarrollo del método, es útil para facilitar cálculos posteriores.

· Ahora queremos obtener el 0 que se ubica en la 3ª fila, 2ª columna de la matriz identidad, para hacer esto buscamos el opuesto del número que se ubica en la 3ª fila, 2ª columna de la matriz con la cual estamos operando, en este caso -17, cuyo opuesto será 17; lo que hacemos ahora es multiplicar este número por todos los elementos de la 2ª fila y sumar esos resultados con el número que le corresponde en columna de la 3ª fila.

· A esta altura podemos observar como la matriz con la cual estamos operando empieza a parecerse a la matriz identidad.

Nuestro siguiente paso es obtener el 1 correspondiente a la 3ª fila, 3ª columna de la matriz identidad, ahora bien, aplicamos el mismo procedimiento con el que estábamos trabajando, es decir que vamos a multiplicar toda la 3ª fila por el inverso del número que se encuentre en la posición de la 3ª fila, 3ª columna, en este caso 96/13, cuyo inverso será 13/96.

· Luego debemos obtener los dos ceros de la tercera columna de la matriz identidad, para lograr esto, buscamos el opuesto de los números que se ubicaron por encima del 1 de la 3ª columna de la matriz con la cual estamos operando, en este caso 11/13 y ½ cuyos opuestos serán - 11/13 y -½, respectivamente.

Una vez hecho esto, se procederá a multiplicar los opuestos de estos números por cada uno de los elemento de la 3ª fila y estos se sumaran a los números de su respectiva columna. Por ej.: en el caso de la 2º fila, se multiplicara a - 11/13 (opuesto de 11/13) por cada uno de los elementos de la 3º fila y se sumaran sus resultados con el número que le corresponda en columna de la segunda fila. En el caso de la 1ª fila se multiplicara a -½ (opuesto de ½) por cada uno de los elementos de la 3º fila y se sumaran sus resultados con el número que le corresponda en columna de la primera fila.

· El último paso que debemos realizar es obtener el 0 de la 1ª columna, 2ª fila de la matriz identidad, para hacer esto buscamos el opuesto del número que se ubica en la 1ª columna, 2ª fila de la matriz con la que estamos operando, en este caso es 3/2, cuyo opuesto será - 3/2, lo que hacemos ahora es multiplicar este número por todos los elementos de la 2ª fila y sumar esos resultados con el número que le corresponde en columna de la 1ª fila.

· Como podemos observar hemos llegado al modelo de la matriz identidad que buscábamos, y en la cuarta columna hemos obtenido los valores de las variables, correspondiéndose de este modo:

x= 1

y= -1

z= 2

· Luego, el sistema de ecuaciones está resuelto y por último lo verificamos.

2x + 3y + z = 1 3x – 2y – 4z = -3 5x – y – z = 4

2*1+3*(-1)+2=1 3*1- 2*(-1)-4*2=-3 5*1-(-1)-2 =4

2 -3 +2 =1 3 +2 - 8= -3 5 +1 - 2 = 4

1 = 1 -3 = -3 4= 4

Tutorial Gauss-Jordan: